yukicoder No.484 収穫

問題

問題概要

i番目の木はA[i]の実が実る. 時刻1で隣の木にいどうすることができる. 移動しなくてもよい. このような条件ですべての実を回収するのにかかる時間の最小値を求める.

解法

区間dpで解けるみたい. 今回の問題を考えるにあたって重要な考察は, i番目の実を回収する時刻はその実を最後に通過するときでよいということである. 実が消えるわけでないので, 最後に訪問するときに回収すれば十分である. このように実を回収するのを最後の訪問時と決めて考えると, 実を回収してない区間が, 連続間であらわすことができるようになる.
dp[l][r][isright] :=
isright = 0のとき　[l+1, r]が未収穫で, lにいるとき
isright = 1のとき　[l, r-1]が未収穫で, rにいるとき
と考えてdpすることができる.
[l, r]が未収穫な時, 未収穫な区間が連続区間になることから, 次に収穫できるセルはlまたはrになる. それを考えて漸化式を立てていけばよい. ただし、lまたはrのセルに達した時点で収穫できる状態になっているかを考えて場合分けしなければならない. 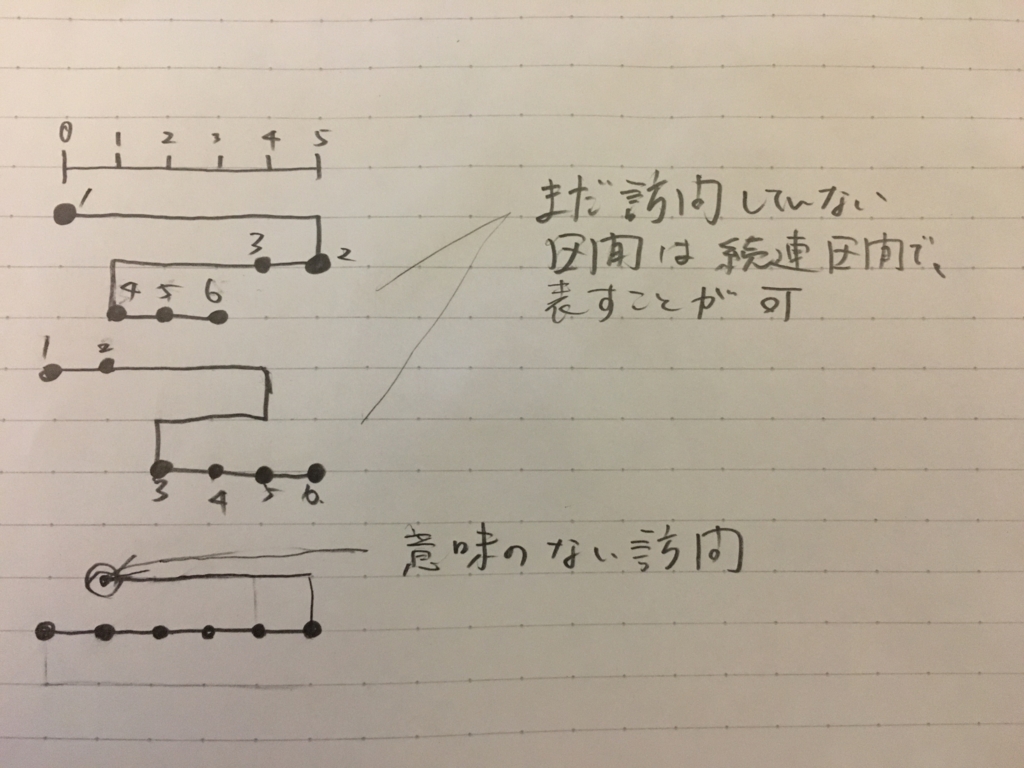上の図は連続区間であることと, 端から始めない場合は一番初めの位置が無駄になることを示している.

区間dp

区間dpてどういうことだろう. ggったら, 区間の包含関係をトポロジカル順序として使っていることが鍵となっていると書かれていた. 確かに今回の問題も区間全体を考えた状態から、区間の右端左端を取り除いた区間へDAGを張ってdpしている. 単純なdpの問題ではi番目までを考えての部分を一番外のループで考えてdpをするが、区間dpでは区間の大きさを考えた部分を一番外のループで考えてやればよいのかな? そうすれば区間の包含関係を考えてDAGを張れるし…?

ミス

初めて区間dpの問題を解いた.　難しいね.

コード

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef vector<int> vint;
typedef pair<int,int> pint;
typedef vector<pint> vpint;
#define rep(i,n) for(int i=0;i<(n);i++)
#define reps(i,f,n) for(int i=(f);i<(n);i++)
#define each(it,v) for(__typeof((v).begin()) it=(v).begin();it!=(v).end();it++)
#define all(v) (v).begin(),(v).end()
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define chmax(a, b) a = (((a)<(b)) ? (b) : (a))
#define chmin(a, b) a = (((a)>(b)) ? (b) : (a))
const int MOD = 1e9 + 7;
const int INF = 1e9;
const ll INFF = 1e18;

//dp[l][r][isright] := 
//isright = 0のとき　[l+1, r]が未収穫で、lにいるとき
//isright = 1のとき　[l, r-1]が未収穫で、rにいるとき
ll dp[2010][2010][2];
int n;
ll a[2010];

signed main(void){
    cin >> n; rep(i, n) cin >> a[i];
    if(n == 1){
        printf("%lld\n", a[0]); return 0;
    }
    rep(i, 2010)rep(j, 2010)rep(k, 2) dp[i][j][k] = INFF;
    dp[0][n - 1][0] = a[0];
    dp[0][n - 1][1] = a[n - 1];
    for (int len = n - 1; len >= 0; --len){
        for (int i = 0; i + len <= n; ++i){
            rep(k, 2){
                //左端が l , 右端が r
                int l = i, r = i + len;
                if(dp[l][r][k] == INFF || l >= r) continue;
                ll time = dp[l][r][k];
                if(k == 0){//現在のセルが　l の時 [l + 1, r]が未収穫
                    //l->l+1
                    if(time + 1 >= a[l + 1]) chmin(dp[l + 1][r][0], time + 1);
                    else chmin(dp[l + 1][r][0], a[l + 1]);
                    //l->r
                    if(time + r - l >= a[r]) chmin(dp[l + 1][r][1], time + r - l);
                    else chmin(dp[l + 1][r][1], a[r]);
                }else{//現在のセルが　r の時 [l, r - 1]が未収穫
                    //r->r-1
                    if(time + 1 >= a[r - 1]) chmin(dp[l][r - 1][1], time + 1);
                    else chmin(dp[l][r - 1][1], a[r - 1]);
                    //r->l
                    if(time + r - l >= a[l]) chmin(dp[l][r - 1][0], time + r - l);
                    else chmin(dp[l][r - 1][0], a[l]);
                }
            }
        }
    }
    ll ans = INFF;
    rep(i, n)rep(j, 2){
        chmin(ans, dp[i][i][j]);
    }
    printf("%lld\n", ans);
    return 0;
}