ABC 219 C - Neo-lexicographic Ordering
問題概要
指定された辞書順で文字列をソートする。
解法
文字列を27進数として考え、数に変換する。文字列の長さが異なるもの同士を比較するときは注意が必要である。
コード
#include <bits/stdc++.h> using namespace std; typedef long long ll; int main () { string x; cin >> x; map<char, int> mp; { for (int i = 0; i < (int)x.size(); ++i) { mp[x[i]] = i + 1; } } int n; cin >> n; vector<string> s(n); { for (int i = 0; i < n; ++i) { cin >> s[i]; } } vector<pair<ll, int>> v; { for (int i = 0; i < n; ++i) { ll val = 0; for (int j = 0; j < 10; ++j) { if (j < (int)s[i].size()) { val = val * 27 + mp[s[i][j]]; } else { val = val * 27; } } v.push_back(make_pair(val, i)); } sort(v.begin(), v.end()); } for (auto u : v) { cout << s[u.second] << endl; } return 0; }
ブレゼンハムアルゴリズム
与えられた始点と終点の間に連続した点を置き、近似的な直線を引くためのアルゴリズムである。y = ax + b を近似する場合、ある整数 x に対して、y の値を計算し、その値を四捨五入して整数値にした値を近似値とすればよい。
この操作を始点から終点までのすべての x に対して行えば良いのだが、それだと無駄な計算が多いので効率化したのがこのアルゴリズムである。
以下にこのアルゴリズムをC言語で実装したプログラムである。line の方は浮動小数点演算を使用して、アルゴリズムをそのまま実装したもので、line_fast は line の中で使われている浮動小数点演算をなくし、整数演算のみで行ったものである。どのようにして浮動小数点演算を整数演算に変換するかだが、
浮動小数点演算が使われているところが整数値になるように、2*dx をかけることで e = e + d と e >= 0.5 が整数演算に置きかわる。
http://sioramen.sub.jp/algorithm-bresenham/bresenham.html
#include <bits/stdc++.h> using namespace std; void plot(int x, int y) { printf("%d %d\n", x, y); } void line(int xa, int xb, int ya, int yb) { assert(xa < xb && ya < yb); int dx = xb - xa; int dy = yb - ya; double d = (double)dy / dx; assert(0. <= d && d < 1.); double e = 0.; int y = ya; for (int x = xa; x <= xb; ++x) { plot(x, y); e = e + d; if (e >= 0.5) { y++; e = e - 1; } } } void line_fast(int xa, int xb, int ya, int yb) { assert(xa < xb && ya < yb); int dx = xb - xa; int dy = yb - ya; assert(dy < dx); int e = 0; int y = ya; for (int x = xa; x <= xb; ++x) { plot(x, y); e = e + 2 * dy; if (e >= dx) { y++; e = e - 2 * dx; } } } int main(int argc, char const *argv[]) { // Ex) (x, y): (2, 3) -> (8, 6); int xa = 2, xb = 8, ya = 3, yb = 6; printf("line\n"); line(xa, xb, ya, yb); printf("\n"); printf("line_fast\n"); line_fast(xa, xb, ya, yb); return 0; }
pthreadによるスレッド間でのカウンタの共有
まず以下のプログラムのように、変数xを複数のスレッドが共有し、それぞれのスレッドがCOUNT_NUM回、変数xをインクリメントする処理を行う。
あるスレッドが(*(int *)i) += 1を実行する間に、他のスレッドも同じ部分を実行すると、競合が起こり、最終的に変数xの値が期待した値と異なる。 以下のプログラムを実行すると、期待した値と異なる結果が出力される。
なぜ競合が起きるのかだが、(*(int *)i) += 1 はソースコードレベルでは1行で表されているコードだが、機械語レベルで考えると、メモリからのロード、値の加算、メモリへのストアの3命令に分割されて実行される。この3命令を一つのスレッドが実行している間に、ほかのスレッドの3命令の実行が行わると、正常なインクリメントができなくなってしまう。
実験的に、COUNT_NUMを1にすると、最終的なxの値は期待した値と同じ値になる。理論的には、TH_NUM個のスレッドがそれぞれ変数xを一回ずつインクリメントとし、クロスオーバーやオーバーラップにより、最終的な値は1からTH_NUMの値すべてになる可能性があると思うのだが、なかなか'x'の値が'TH_NUM'以外にならなかった。これはスレッド1のpthread_createをして、次のスレッド2のpthread_createを行いスレッド2が(*(int *)i) += 1を実行するまでの間に、すでにスレッド1の (*(int *)i) += 1 が完全に終了しているからだろうか??
// gcc -std=c11 -pthread no_mutex.c #include <stdio.h> #include <pthread.h> #define TH_NUM 10 #define COUNT_NUM 10000 void *add(void *i) { for (int k = 0; k < COUNT_NUM; k++) (*(int *)i) += 1; // count up return NULL; } int main() { int x = 0; // shared value pthread_t th[TH_NUM]; for (int n = 0; n < TH_NUM; n++) pthread_create(&th[n], NULL, add, &x); for (int n = 0; n < TH_NUM; n++) pthread_join(th[n], NULL); printf("actual: %d, expected: %d\n", x, COUNT_NUM * TH_NUM); return 0; }
次に、必ず期待した値になるように、mutexを使って、複数のスレッドが同時にクリティカルセクション(ここでは(*(int *)i) += 1の命令の実行開始から終了まで)へ入ることを防ぐようにコードを変更した。それが以下のようになる。
// gcc -std=c11 -pthread mutex.c #include <stdio.h> #include <stdatomic.h> #include <pthread.h> #define TH_NUM 10 #define COUNT_NUM 10000 struct params { int *i; pthread_mutex_t *mut; }; void *add(void *arg) { struct params* prm = (struct params *)arg; for (int k = 0; k < COUNT_NUM; k++) { pthread_mutex_lock(prm->mut); (*(int *)(prm->i)) += 1; // count up pthread_mutex_unlock(prm->mut); } return NULL; } int main() { int x = 0; // shared value pthread_t th[TH_NUM]; pthread_mutex_t mut = PTHREAD_MUTEX_INITIALIZER; struct params prm = {&x, &mut}; for (int n = 0; n < TH_NUM; n++) pthread_create(&th[n], NULL, add, &prm); for (int n = 0; n < TH_NUM; n++) pthread_join(th[n], NULL); printf("actual: %d, expected: %d\n", x, COUNT_NUM * TH_NUM); return 0; }
参考
store to load forwarding
あるメモリアドレスに書き込む命令の後に同じアドレスから読み込む命令が続くとき, store forwarding が行われる.
mov DWORD [esi], edi mov eax, DWORD [esi]
上の例だと1行の書き込みが実際にL1$に書き込む前に, Store Bufferに書き込まれ, 読み込む命令はL1$にアクセスせずに, Store Bufferにあるデータを利用して処理を行う.
mov WORD [esi], di ; small write mov eax, DWORD [esi] ; big read (stall)
上のような読み込むサイズが書き込みサイズより大きい場合は, forwardingは行われない.
Ref
Store forwarding by example. | Denis Bakhvalov | C++ compiler dev.
main()の前後で関数を呼び出す
#include <stdio.h> __attribute__((constructor)) void foo() { printf("hello, before main\n"); } __attribute__((destructor)) void bar() { printf("hello, after main\n"); } int main(int argc, char const *argv[]) { printf("hello, world\n"); return 0; }
$ gcc test.c $ ./a.out hello, before main hello, world hello, after main
CPUキャッシュの最適化について
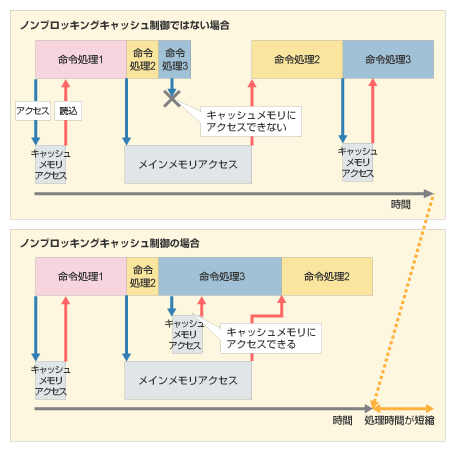
Non-blocking Cache
キャッシュメモリの構成法の一つであり, キャッシュミスが起こり, それが処理されている最中でも, cache アクセスを可能にする. さらにメモリレベルの並列性(Memory-level parallelism) を使用することで, 同時に複数のキャッシュミスを処理することできる.
Non-blocking Cacheが必要な理由を説明する. 現在のCPUは Out of Order で実行されているため, ある命令によりキャッシュミスが発生しても, 次の命令を実行することができる. その命令がメモリアクセスが必要ならば, キャシュにアクセスする必要があるが, Blocking Cache であればそこで命令の実行が止まってしまう. しかし, Non-blocking Cache であれば命令を完了することができたり, Cacheでデータがヒットしなかった場合でも, 前のキャッシュミスと並列にミスを処理することを可能にするため, メモリアクセスのレイテンシを小さくすることができる.
Miss-Status Holding Registers (MSHR)
miss bufferと呼ばれており, 未処理のキャッシュミスを追跡するためのハードウェアである. キャッシュミスが起きたとき, MSHRはその要求されたキャッシュラインがすでにメモリからキャッシュへフェッチしようとしている最中かどうかを判断するのに使われる. (Non-blocking Cacheであればキャッシュミスの処理最中に後続の命令で同じメモリアドレスを要求してくることがあり得る.) もしすでに同じアドレスのミスを処理中であれば, この要求がMSHRのおなじエントリに併合され, 新しい要求を生成しないようにする. (する必要がない.) そうでなければ, 新しいMSHRのエントリをアロケートして, キャッシュラインの要求が予約される. 空きのMSHRがない場合は, ストールする.
https://www.cse.iitk.ac.in/users/biswap/CS422/L18-CO.pdf
Victim Cache
従来のものは, コアからのメモリアクセス要求に対しては, 1, 2, 3次と順にキャッシュをチェックし, それでもミスした場合は, メモリからデータを読み込む. メモリから読み込まれたデータは 3, 2, 1次キャッシュと順に格納され, コアにデータが送られることになる. これに対して, 1,2,3次と順にチェックするが, データを3,2次に書き込まずに, 直接1次にデータを書き込み, 書き込みによって追い出されるデータを2次に書き込む方式を victim cache という.
従来のキャッシュであれば, L1のデータはL2に存在し, L2のデータはL3に存在するという包含関係が存在した. これを Inclusion Cache という. 一方で, Victim Cache の場合そのような包含関係は存在しないので, Non Inclusion Cache という.
自己書き換えコード(self-modifying code)
自己書き換えコードとは, 実行時に自分自身の命令を書き換えるコードのことである.
以下のコードでは, foo() 関数の i++ の命令を i += 2に自己書き換えしている.
順に説明していくと, まず mprotect() 関数でfoo関数の命令が書かれているページに読み, 書き, 実行の権限を与える. foo() 関数を書き換えるので, 書き換え権限を与えなければならない. 通常セキュリティーの観点から関数などのコードが書かれている領域は書き込み権限がない.
次に, 普通に foo() を呼び出した後, foo() 関数の先頭から 18 byte進んだ位置のbyteに 0x2 を書き込んでいる. これは foo() のアセンブラを見ればわかるように, 18 byteのところが add DWORD PTR [rbp-0x4],0x1 の 0x1 に対応しているので, そこを 0x2 に書き換えている.
これで自己書き換えができたので, その後に foo を呼び出すと出力結果が変わる.
プログラム
#include <stdio.h> #include <stdlib.h> #include <unistd.h> #include <sys/mman.h> void foo() { int i = 0; i++; printf("i: %d\n", i); } /* 000000000000072a <foo>: 72a: 55 push rbp 72b: 48 89 e5 mov rbp,rsp 72e: 48 83 ec 10 sub rsp,0x10 732: c7 45 fc 00 00 00 00 mov DWORD PTR [rbp-0x4],0x0 739: 83 45 fc 01 add DWORD PTR [rbp-0x4],0x1 73d: 8b 45 fc mov eax,DWORD PTR [rbp-0x4] 740: 89 c6 mov esi,eax 742: 48 8d 3d 4b 01 00 00 lea rdi,[rip+0x14b] # 894 <_IO_stdin_used+0x4> 749: b8 00 00 00 00 mov eax,0x0 74e: e8 8d fe ff ff call 5e0 <printf@plt> 753: 90 nop 754: c9 leave 755: c3 ret */ int main() { int page_size = getpagesize(); void *foo_addr = (void*)foo; printf("foo_addr: %p\n", foo_addr); void* page_addr = (void*)((unsigned long)(foo_addr) & ~(page_size - 1)); printf("page_addr: %p\n", page_addr); mprotect(page_addr, page_size, PROT_READ|PROT_WRITE|PROT_EXEC); printf("Call original foo()\n"); foo(); // Change code // add DWORD PTR [rbp-0x4],0x1 => add DWORD PTR [rbp-0x4],0x2 ((unsigned char*)foo_addr)[18] = 0x2; printf("Call modified foo()\n"); foo(); return 0; }
出力結果
foo_addr: 0x555992c1672a page_addr: 0x555992c16000 Call original foo() i: 1 Call modified foo() i: 2